[案例]寓学于乐?融数于趣

张伟

摘要：小学阶段以探究活动为主要特点的“探索规律”课，是学生可以在数学活动中探寻数学问题，在实际操作中发展数学能力的学习活动。其教学路径有：唤醒与激活，让学生自主参与到数学探究活动中去;引导与启发，让学生始终处于探究与思考的学习状态;啟智与做中学，让学生达成寓学于乐、融数于趣的学习体验。

关键词：探究学习;数学活动;做中学

中图分类号：G623.5 文献标志码：A 文章编号：1673-9094（2020）12B-0052-04

作为小学数学课程的重要组成部分，“探索规律”课设置的目的在于使学生在探索规律、发现规律和表达规律的过程中，感受数学抽象的意义，培养比较、分析、推理的能力，发展问题意识和创新意识，积累数学活动经验，是一类以探究问题为载体、以学生自主参与为主的学习活动。“钉子板上的多边形”是小学数学苏教版五年级上册一节典型的“探索规律”课，其教学目标是让学生探索并发现钉子板上围成的多边形面积，与围成的多边形边上的钉子数及多边形内部的钉子数之间的规律，并尝试用含有字母的式子表示出几者间的关系。在此过程中，学生经历观察、操作、实验等探究活动，发展归纳、概括、抽象、建模的能力，促进问题意识与创新意识的养成。

教学实际中，不少同学对用钉子数来求解多边形面积的方法掌握得不好，对研究过程及方法由来不甚了解。究其原因，我们发现教材编写者意图让学生通过开展数学活动探究出钉子数与多边形面积之间的关系，但是编排时比较刻板，先围绕图形内只有1枚钉子的情况来开展探索，然后又组织学生探究图形内只有2枚钉子的情况，最后让学生思考“如果多边形内有3枚、4枚……钉子，它的面积与它边上的钉子数的关系怎么变化？”，每次都是先让学生在组内说想法，再动手探究。整个教学设计环节过多，用时过长，且存在重复探究现象。几个探究活动看似开放，但执行起来还是按照线性流程执行，学生难免会感到兴味索然，疲于配合。如何改变以上现状，让学生真正参与到探索规律的活动中去呢？

一、注重唤醒与激活，让学生自主参与到数学探究活动中去

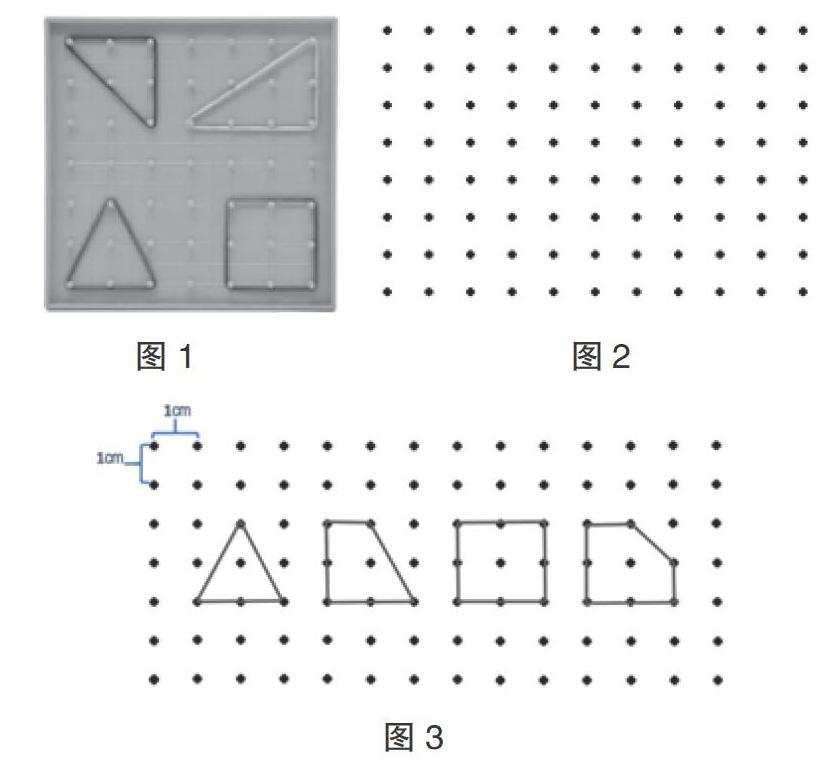
小学阶段的学生葆有儿童特有的童真童趣，平时就十分喜爱参与游戏活动。课始，教师可以组织师生间开展轻松谈话，唤醒学生已有经历与经验，从而更好地对接新知。比如本课可以先与孩子交流有无玩过钉子板，再组织学生实际动手操作，利用钉子板开展围图数学游戏活动，在钉子板上围出不同的多边形来（如图1）。紧接着，告知学生在数学上可以用格点图（如图2）的形式来代替钉子板，在格点图上可以继续玩围多边形的游戏，指导学生尝试在格点图上用铅笔和直尺画出几个多边形。接着，选取一些玩游戏时格点图上出现过的多边形，组织学生计算各图形的面积（如图3）。师生交流发现各图形的面积，既可以借助底、高、边长等条件，通过“计算”求出来，也可以结合格点图，通过“数方格”得出结果。

这样的设计，在调动学生参与热情的同时，不知不觉中抽象出格点图，很自然地过渡到如何用数学的方法去解决游戏中出现的数学问题，学生易于理解、乐于尝试，也为进一步的探究活动积累了丰富的操作经验。

二、注重引导与启发，让学生始终处于探究与思考的学习状态

数学规律具有抽象性，往往都比较隐蔽，藏在众多现象与复杂情境中。只有经过主观上的有意注意才会关注到规律（即共性）的存在，经过思考还会发现数学规律也有局限性。如本课中多边形内部钉子数不同时，蕴含的规律也存在着不同。学生在进行探究时，教师应注重启迪引导，让学生合理分类、适时聚焦，将研究的关注点放到简单易探究的问题上来。通过充分的探究、师生的交流，培养学生掌握探究问题的一般方法，并鼓励学生以自主、合作、开放的姿态，投入到其他类具有挑战性的问题研究中去，让学生始终处于探究与思考的学习状态。

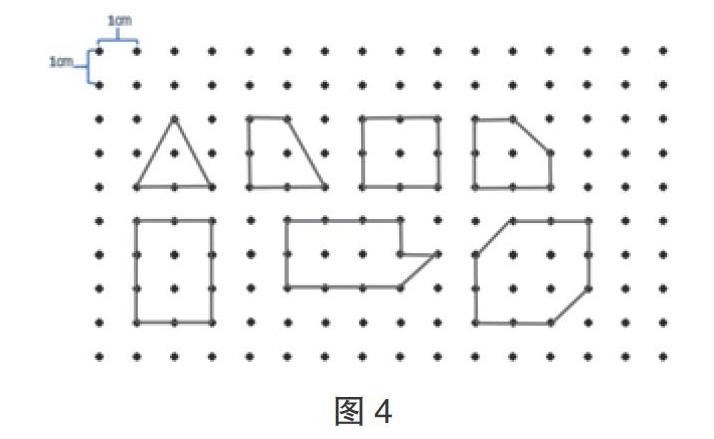
当学生掌握用“计算”“数方格”的方法求多边形面积后，教师在格点图上出示更多的多边形（如图4），启发学生换个角度思考：“多边形面积大小还可能和什么有关？”学生通过积极讨论后得出了“多边形的面积可能与多边形边上以及里面的钉子数有关”的结论，从而进一步明晰了探索、研究的方向。

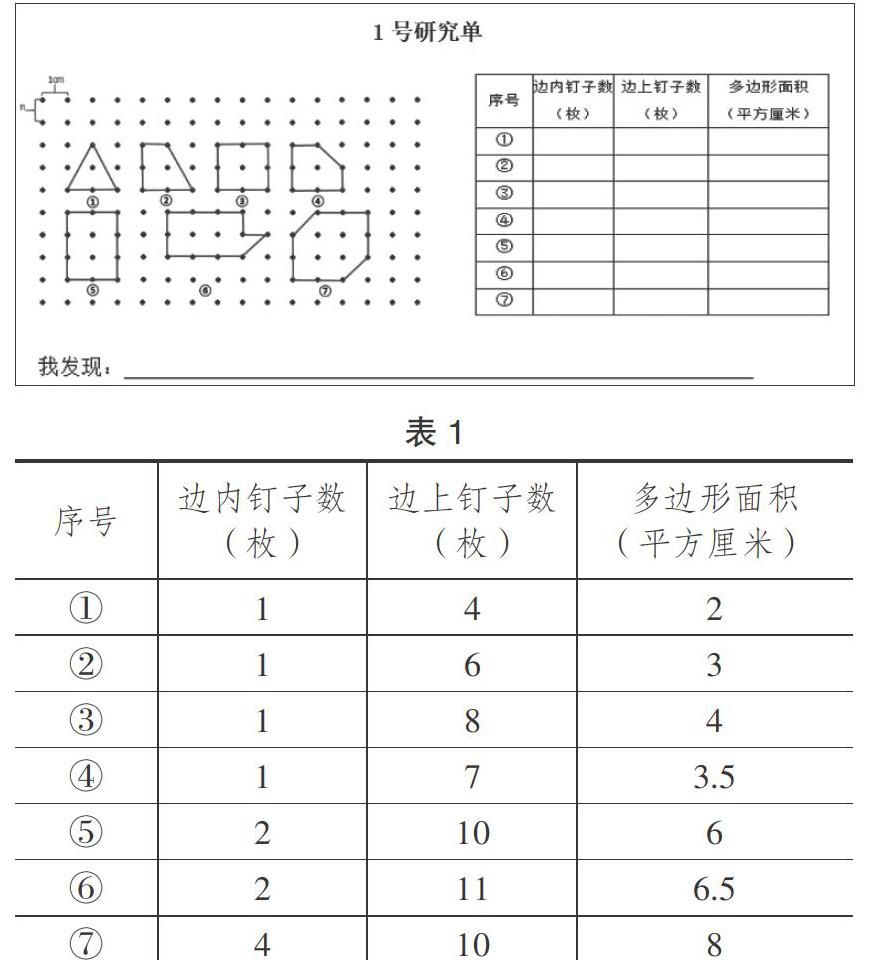
接着，教师组织学生运用合理的方法得出格点图上7个多边形的面积，填写1号研究单，得到表1中的数据。

教师进一步引导学生发现钉子数与面积之间的规律：①、②、③、④号多边形的面积都等于边上钉子数除以2，两者在数值上存在两倍的关系。但是这样的规律在⑤、⑥、⑦号多边形上却不存在。通过观察与比较，学生发现①、②、③、④号多边形之间存在着共性，即内部只有1枚钉子。在此情况下，教师启发学生猜想：多边形内部只有1枚钉子时，多边形面积等于边上钉子数除以2，并继续引导学生小心求证，通过举例验证来判断这个猜想正确与否，且鼓励学生积极寻找反例。最终，学生得出了这样的结论：当多边形的内部只有1枚钉子，多边形面积等于边上钉子数除以2。教师进一步鼓励学生尝试运用符号来进行表征，初建模型。用 S 表示多边形的面积，n表示多边形边上的钉子数，这个规律可以表示为S=n÷2。

当学生完成以上探究后，他们自然对多边形内部有 0 枚、2 枚、3 枚、4 枚……钉子数的情况产生了浓浓的探究欲望。此时，回顾探究过程，交流探究方法，能更好地帮助学生建立认知，掌握自主操作探究的方法。具体的探究方法为：①确定好一类研究对象（即内部钉子数相同的多边形）;②“算出”或“数出”多边形的面积、边上钉子数、内部钉子数;③通过观察归纳，形成“猜想”，再任意举例“验证”猜想，尝试寻找有无反例;④用字母式来表示探索出的规律。接着，教师出示 2 号研究单及活动要求，再次组织学生进行自主探究活动。全班交流时，学生汇报展示各组数据，并揭示各组发现的规律（用字母式表达），整理出表2。最终，学生通过对表格中数据的观察与比较，发现多边形面积与边上钉子数与内部钉子数均存在着一定的规律。当用字母a表示边内的钉子数时，可以归纳概括出更具普适性的规律：S= n÷2+a-1。

三、注重启智与做中学，让学生达成寓学于乐、融数于趣的学习体验

陈省身曾经提过“数学好玩”这样的观点，但在平时的教学过程中，学生哪能轻易体会到数学好玩呢？不仅不好玩，而且学得累得很。从学科特点来说，数学知识是比较抽象的，具有高度的概括性，不像其他学科知识那样形象、生动、直观，学生在学习数学时常常会感觉到枯燥、无味、无趣。所以，教师在进行教学设计时，要努力让学生亲近数学，走进数学。作为探索规律课，教学时应该特别注重在实际操作中帮助学生体会方法，体悟思辨，通过猜想、实验、计算、推理、验证等探究活动，让学生结合学具材料，手、脑、口并用，丰富寓学于乐、融数于趣的学习体验。

1.寓学于乐，以玩启智

著名心理学家皮亚杰提出，儿童需要游戏，游戏可以帮助他们解决与外部世界的冲突。以数学活动为主要特点的探索规律课就应该让儿童在游戏玩耍中探寻数学问题，可以自己算一算、数一数，也可以相互猜一猜、说一说，共同画一画、填一填等。要让儿童运用多种学习方式参与活动、参与探究，让学生在习得知识技能的同时，感悟数学思想方法，发展数学思维能力。本课中的钉子板学生平时就接触过，并不陌生，有时学生还把钉子板作为玩具来玩，拼出自己喜歡的各种图案来。教师从钉子板引入格点图，再在格点图上研究多边形面积，学生自然进入了类似游戏活动的情境。在此情境下研究平面图形的面积，既有趣，又有挑战性。学生们可以利用格点图，先得出多边形的边长，再借助面积计算公式“算”出面积;也可以利用格点围成的面积单位“数”出面积。相对而言，“数”的方法会更快捷一些，并且更有趣味一点，尤其是不满格部分的面积有时还存在着多样化的数法。接着，教师启发学生思考多边形的面积还可能与什么有关，让学生大胆猜测，将思考点放在多边形边上及里面的钉子数上，而数钉子的枚数、算图形的面积，这些都是学生喜欢做、能够做的事情，他们会乐意参与这样类似游戏的活动。在此过程中，教师要适时引导学生在游戏活动中开展数学思考：“我们有什么发现？”“这个发现一直存在吗？”“分分类，发现这一规律存在于哪几个多边形中？”“你有什么猜想？”“如何验证？”这些问题的思考会促使学生逐步将注意力从游戏的趣味性转向对规律的探究上来，进而感受到玩中有智，学中有乐，体验到数学规律的探究是大有乾坤、精彩纷呈的。

2.融数于趣，在做中学

2011年版的数学课程标准倡导通过动手实践、自主探索、合作交流来开展学习，这与著名教育家杜威先生提出的“做中学”的理念不谋而合。“钉子板上的多边形”教学之前，学生已经较好地形成了面积概念，掌握了常用面积单位，能计算简单的平面图形面积。但是，在钉子板上围出来的图形比较有趣，大多数不是规则图形，也不是简单图形，求它们的面积没有现成的方法可以使用，得出图形的面积比较难。学生不会轻易想到围成的多边形面积与边上的钉子数、里面的钉子数之间的关系，并且用高度抽象的含有字母的式子表达这种关系，也是有难度的。也正是因为这些“趣”与“难”，有助于体现动手操作活动的教育价值，通过“做中学”，培养学生的探索精神与实践能力，发展学生的数学思考能力。

在探究多边形面积规律的过程中，动手操作始终发挥着重要的作用，引领着学生充分经历观察、计算、猜测、归纳、验证等思维活动，形成了开放、多元、合作的课堂研究氛围。借助实际操作要求，在初步掌握探究图形内部只有1枚钉子的规律后，每一组都自主选择了一类喜欢探究的情况，组内每一位学生都经历了完整的研究过程，较好地掌握了规律探究中特有的“先猜想，再验证”的研究方法，为后期持续学习与研究打下了基础。不管是分组探究，还是大组交流，都会产生一组组实验操作的数据，在繁杂的数据里观察、思考、发现，成了寻找规律的有效途径，也成了数学探究的乐趣源泉。同时，小组的分类探究与大组的分享汇报也帮助学生积累了更多数学活动的基本经验。这里的经验既有外显的操作经验，如画一画、算一算、数一数，也有内隐的思维经验，如猜想验证、联想类比、建立模型等。从中不难看出，开放民主的教学理念、精心巧妙的教学设计、广泛参与的学生状态、适时恰当的教学引领是组织好学生动手实践、从做中学的关键。

责任编辑：丁伟红

Abstract： The “exploratory law” class with inquiry activities as the main feature at the elementary school level is a learning activity where students can explore mathematical problems in mathematical activities and develop their mathematical abilities in practical operations. The teaching path includes： awakening and activation， allowing students to participate in mathematics inquiry activities independently; guiding and enlightening， so that students are always in a learning state of inquiry and thinking; enlightenment and learning by doing， so that students can achieve an interesting learning experience with learning integrated with enjoyment.

Key words： inquiry learning; mathematical activities; learning by doing

本文由： 乡镇企业导报杂志社编辑部整理发布，如需转载，请注明来源。

乡镇企业导报杂志社编辑部

2021/09/28